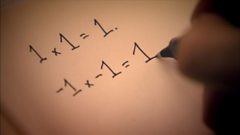Â鶹¹ÙÍøÊ×Ò³Èë¿Ú

Marcus du Sautoy explores how simple rules can give rise to very complex shapes in natural systems. He begins by looking at trees, and uses a computer simulation to show how they grow and branch and – with a little natural variation thrown in – become fully grown. Mandelbrot's ideas of infinitely complex fractals are then shown. Du Sautoy then visits Pixar, where he is shown how fractals were used to create some of the very first 'realistic' digital animations. Starting with a very low resolution landscape, simple fractal rules are used to make highly complex and natural looking scenes. Since then, all Pixar films have used fractal mathematics to animate surfaces and textures.